题目大意

给出两把梯子的高长度 $x$ 和 $y$，以及交叉点 $c$ 的高度，求道路的宽（即两梯子底端之间的距离）。

解题思路

数学 + 二分

可以利用梯子的长度和梯子与地面的夹角来求得道路的宽。

设梯子 $x$ 与 $y$ 与地面的夹角分别为 $\alpha$ 和 $\beta$，道路的宽设为 $w$，梯子 $x$ 的底端与交叉点在地面的水平投影距离为 $h$。

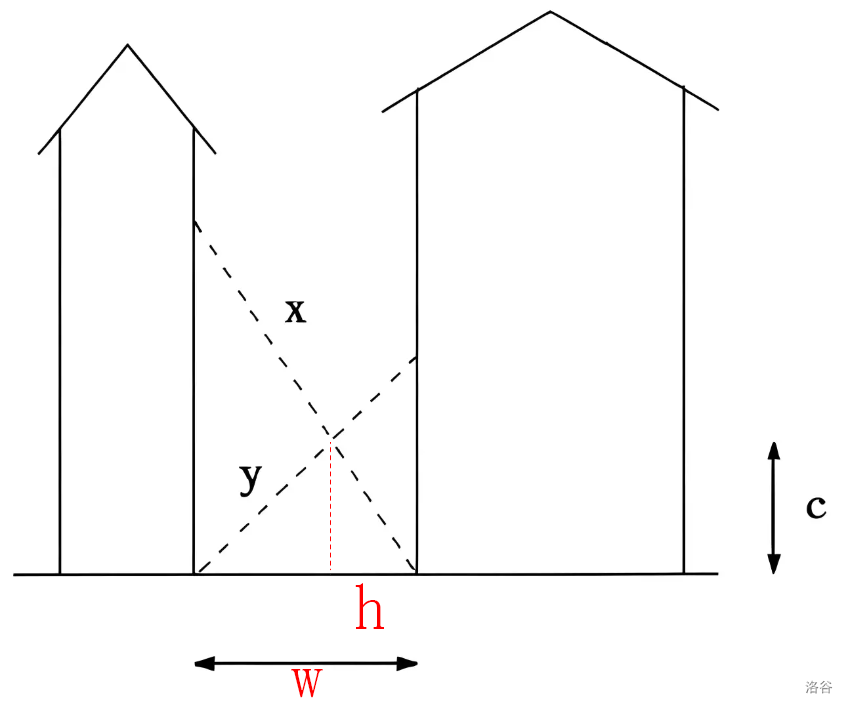
则有 $\sin(\alpha)=\frac{c}{x}$，$\sin(\beta)=\frac{c}{y}$，$\cos(\alpha)=\frac{w+h}{x}$，$\cos(\beta)=\frac{w}{y}$。

解出 $h$ 为：
$\displaystyle h=y\times\cos(\beta)=y\times\sqrt{1-\sin^2(\beta)}=y\times\sqrt{1-\frac{c^2}{y^2}}=y\times\frac{\sqrt{y^2-c^2}}{y}=\sqrt{y^2-c^2}$
并表示道路宽 $w$ 为：
$\displaystyle w=x\times\cos(\alpha)-h=x\times\sqrt{1-\sin^2(\alpha)}-h=x\times\sqrt{1-\frac{c^2}{x^2}}-h=x\times\frac{\sqrt{x^2-c^2}}{x}-h=\sqrt{x^2-c^2}-h$
将 $h=\sqrt{y^2-c^2}$ 代入，得：
$\displaystyle w=\sqrt{x^2-c^2}-\sqrt{y^2-c^2}$
不难看出，该解析式具有单调递减性，又由于数据为实数，则可以使用实数二分，不断逼近所需精度。

代码

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define int long long
#define endl "\n" 
using namespace __gnu_cxx;
using namespace __gnu_pbds;
using namespace std;
double x,y,c;
inline bool check(long double m)//检查函数
{
    long double h1=sqrt(x*x-m*m);
    long double h2=sqrt(y*y-m*m);
    return (h1*h2)<(h1*c+h2*c);//返回精度偏小（true）还是偏大（false）。
}
signed main() 
{
    while(cin>>x>>y>>c)
    {
        long double l=0,r=min(x,y);//左右端点
        long double m;
        while(r-l>=1e-6)//实数二分
        {
            m=(l+r)/2;//注意 double 类型不能用右移运算
            if(check(m))r=m;
            else l=m;
        }
        cout<<fixed<<setprecision(3)<<l<<endl;
    }
    return 0;
}