问题描述

将一个后缀表达式（逆波兰表示法）转换成另一种形式，使得使用队列进行计算的结果与使用栈计算原表达式的结果相同。

思路

1. 构建表达式树：从左到右读取输入的后缀表达式，构建一个二叉表达式树。
2. bfs 遍历：对构建好的表达式树进行广度优先搜索。
3. 反转结果：将遍历的结果反转，就得到了最终答案。

BFS 反转分析

1. 初始状态

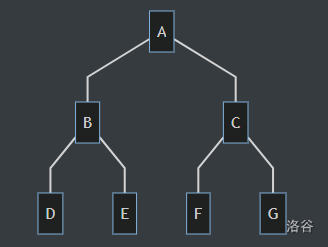
表达式树根节点为 A，其他节点按层次排列。

2. BFS 第一层

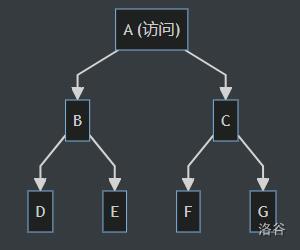
第一步，访问根节点 A。将 A 的值添加到结果字符串中，并将 A 的子节点 B 和 C 加入队列。

3. BFS 第二层

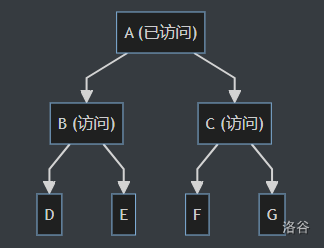
接下来访问 A 的子节点 B 和 C。将 B 和 C 的值添加到结果字符串中，并将它们的子节 D、E、F 和 G 加入队列。

4. BFS 第三层

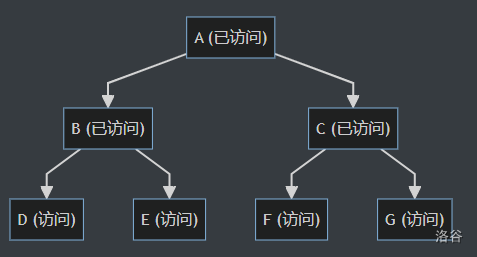
最后访问 B 和 C 的子节点 D、E、F 和 G。将它们的值添加到结果字符串中。由于这些节点没有子节点，跳出递归。

5. 最终结果

BFS 遍历的结果字符串为：ABCDEFG。

将这个结果反转后，得到最终答案：GFEDCBA。

这个反转后的字符串就是我们需要求的，使用队列计算时与原后缀表达式使用栈计算结果相同的新表达式。

代码实现

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#define int long long
using namespace std;
using namespace __gnu_pbds;
struct Node 
{
    char value;
    Node *left,*right;
    Node(char v):value(v),left(nullptr),right(nullptr){}
};
Node* build(const string& expr)//建树
{
    stack<Node*>st;
    for (char c:expr) 
    {
        Node* node=new Node(c);
        if(isupper(c))
        {
            node->right=st.top();st.pop();
            node->left=st.top();st.pop();
        }
        st.push(node);
    }
    return st.top();
}
string bfs(Node* root)//bfs 遍历搜索
{
    string ans;
    queue<Node*>q;
    q.push(root);
    while(!q.empty()) 
    {
        Node* node=q.front();q.pop();
        ans+=node->value;
        if(node->left) q.push(node->left);
        if(node->right) q.push(node->right);
    }
    return ans;
}
signed main() 
{
    int T;
    cin>>T;
    while(T--)
    {
        string expr;//表达式
        cin>>expr;
        Node* root=build(expr);
        string ans=bfs(root);
        reverse(ans.begin(),ans.end());//翻转
        cout<<ans<<endl;
    }
    return 0;
}

时间复杂度

构建表达式树和层序遍历的时间复杂度都是 $O(n)$，其中 $n$ 是表达式的长度。